线性回归
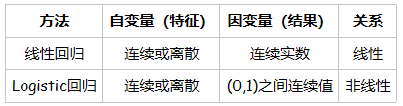
用一组变量的(特征)的线性组合,来建立与结果之间的关系。
模型表达:$y(x, w)=w_0+w_1x_1+…+w_nx_n$
逻辑回归
逻辑回归用于分类,而不是回归。
在线性回归模型中,输出一般是连续的, 对于每一个输入的x,都有一个对应的输出y。因此模型的定义域和值域都可以是无穷。
但是对于逻辑回归,输入可以是连续的[-∞, +∞],但输出一般是离散的,通常只有两个值{0, 1}。
这两个值可以表示对样本的某种分类,高/低、患病/ 健康、阴性/阳性等,这就是最常见的二分类逻辑回归。因此,从整体上来说,通过逻辑回归模型,我们将在整个实数范围上的x映射到了有限个点上,这样就实现了对x的分类。因为每次拿过来一个x,经过逻辑回归分析,就可以将它归入某一类y中。
逻辑回归与线性回归的关系
可以认为逻辑回归的输入是线性回归的输出,将逻辑斯蒂函数(Sigmoid曲线)作用于线性回归的输出得到输出结果。
线性回归y = ax + b, 其中a和b是待求参数;
逻辑回归p = S(ax + b), 其中a和b是待求参数, S是逻辑斯蒂函数,然后根据p与1-p的大小确定输出的值,通常阈值取0.5,若p大于0.5则归为1这类。
具体的:
线性函数如下:
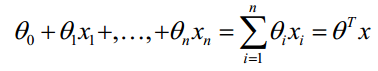
构造预测函数:
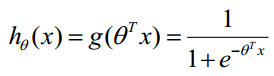
逻辑回归的损失函数:
逻辑回归采用交叉熵作为代价函数,即对数损失函数。能够有效避免梯度消失.
对数损失函数(logarithmic loss function) 或对数似然损失函数(log-likehood loss function):
逻辑回归中,采用的是负对数损失函数。如果损失函数越小,表示模型越好。
极大似然估计:
极大似然原理的直观想法是,一个随机试验如有若干个可能的结果A,B,C,… ,若在一次试验中,结果A出现了,那么可以认为实验条件对A的出现有利,也即出现的概率P(A)较大。一般说来,事件A发生的概率与某一未知参数θ有关, θ取值不同,则事件A发生的概率也不同,当我们在一次试验中事件A发生了,则认为此时的θ值应是一切可能取值中使P(A|θ)达到最大的那一个,极大似然估计法就是要选取这样的θ值作为参数的估计值,使所选取的样本在被选的总体中出现的可能性为最大。
在逻辑回归中目标函数均为最大化条件概率p(y|x),其中x是输入样本
似然:选择参数使似然概率p(y|x,)最大,y是实际标签
过程:目标函数→单个样本的似然概率→所有样本的似然概率→log变换, 将累乘变成累加→负号, 变成损失函数
选择一组参数使得实验结果具有最大概率。
损失函数的由来:
已知估计函数为:
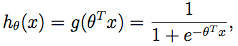
则似然概率分布为(即输出值为判断为1的概率,但在输出标签值时实际只与0.5作比较):
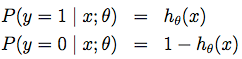
可以写成概率一般式:
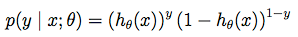
由最大似然估计原理,我们可以通过m个训练样本值,来估计出值,使得似然函数值(所有样本的似然函数之积)最大
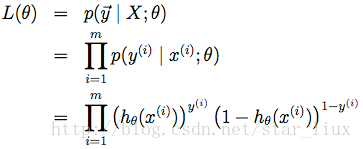
求log:
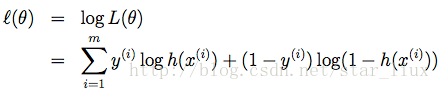
取负数,得损失函数:
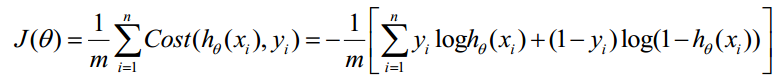
逻辑回归参数迭代,利用反向传播进行计算:
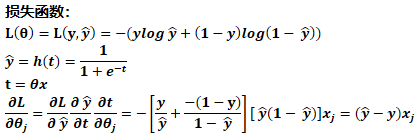
上面这个过程计算的是单个样本对wj的梯度更新。
为什么逻辑回归采用似然函数,而不是平方损失函数?
可以从两个角度理解。
交叉熵损失函数的好处是可以克服方差代价函数更新权重过慢的问题(针对激活函数是sigmoid的情况)。
原因是其梯度里面不在包含对sigmoid函数的导数:
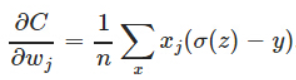
而如果使用的是平方损失函数加sigmoid函数,则计算梯度时:
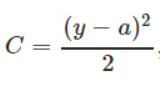
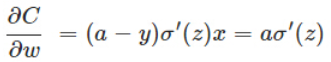
会包含sigmoid的导数(sigmoid的导数值始终小于1),使梯度下降变慢。

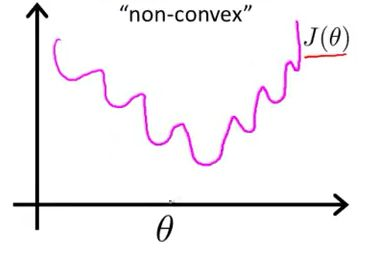
图1 最小二乘作为逻辑回归模型的损失函数(非凸),theta为待优化参数
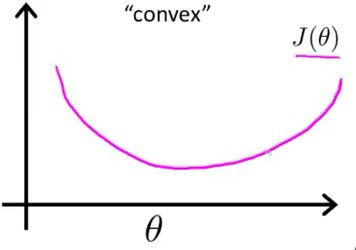
图2 最大似然作为逻辑回归模型的损失函数,theta为待优化参数
逻辑回归为什么使用sigmoid函数
也可以从两点来进行理解
Sigmoid 函数自身的性质
因为这是一个最简单的,可导的,0-1阶跃函数
sigmoid 函数连续,单调递增
sigmiod 函数关于(0,0.5) 中心对称
对sigmoid函数求导简单
逻辑回归函数的定义

因此, 逻辑回归返回的概率是指判别为1类的概率.
逻辑回归和SVM的异同点
相同点:
第一,LR和SVM都是分类算法。
第二,如果不考虑核函数,LR和SVM都是线性分类算法,也就是说他们的分类决策面都是线性的。
第三,LR和SVM都是监督学习算法。
第四,LR和SVM都是判别模型。
判别模型会生成一个表示P(Y|X)的判别函数(或预测模型),而生成模型先计算联合概率p(Y,X)然后通过贝叶斯公式转化为条件概率。简单来说,在计算判别模型时,不会计算联合概率,而在计算生成模型时,必须先计算联合概率。
不同点:
第一,本质上是其loss function不同
逻辑回归的损失函数是交叉熵函数:
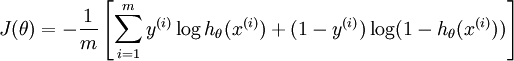
SVM的损失函数:
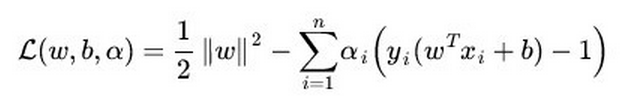
逻辑回归方法基于概率理论,假设样本为1的概率可以用sigmoid函数来表示,然后通过极大似然估计的方法估计出参数的值;
支持向量机基于几何间隔最大化原理,认为存在最大几何间隔的分类面为最优分类面;
第二,支持向量机只考虑局部的边界线附近的点,而逻辑回归考虑全局(远离的点对边界线的确定也起作用)。
第三,在解决非线性问题时,支持向量机采用核函数的机制,而LR通常不采用核函数的方法。
这个问题理解起来非常简单。分类模型的结果就是计算决策面,模型训练的过程就是决策面的计算过程。通过上面的第二点不同点可以了解,在计算决策面时,SVM算法里只有少数几个代表支持向量的样本参与了计算,也就是只有少数几个样本需要参与核计算(即kernal machine解的系数是稀疏的)。然而,LR算法里,每个样本点都必须参与决策面的计算过程,也就是说,假设我们在LR里也运用核函数的原理,那么每个样本点都必须参与核计算,这带来的计算复杂度是相当高的。所以,在具体应用时,LR很少运用核函数机制。
第四,SVM的损失函数就自带正则
参考:
Poll的博客:www.cnblogs.com/maybe2030/p/5494931.html
逻辑回归:https://www.cnblogs.com/Belter/p/6128644.html
逻辑回归推导:http://blog.csdn.net/pakko/article/details/37878837
极大似然估计:http://blog.csdn.net/star_liux/article/details/39666737
刘建平:https://www.cnblogs.com/pinard/p/6035872.html
逻辑回归和SVM的比较:https://www.cnblogs.com/zhizhan/p/5038747.html